백준 1004번 어린왕자
풀이하기 전에 말할 것이 있다. 내가 직접 풀어낸 방식이고 이보다 더 좋은 방법도 있을 수 있고 내 설명이 틀릴 수도 있다.(창피하지만 틀린 점이 있다면 댓글 부탁드립니다.)
이번 문제도 문제를 읽고 이해하려면 시간이 걸린다...
백준 문제는 어떤 값이 입력되며 어떤 값을 출력해야 하는가를 중점으로 봐야 이해가 빨라진다.
즉 문제를 읽고 나서 이해하려고 시간을 들이지 말고 어떤 값이 입력되며 출력되는지를 파악하면 전체 문제를 이해하는 시간이 많이 단축된다.
최단 루트를 구해서 행성을 빠져나가고 들어가기를 몇 번 하는지 구하는 줄 알았다. 하지만 입출력 값을 보면 그럴 필요가 없다. 그냥 몇 번 빠져나가고 들어가야 하는가만 구할 뿐이다.
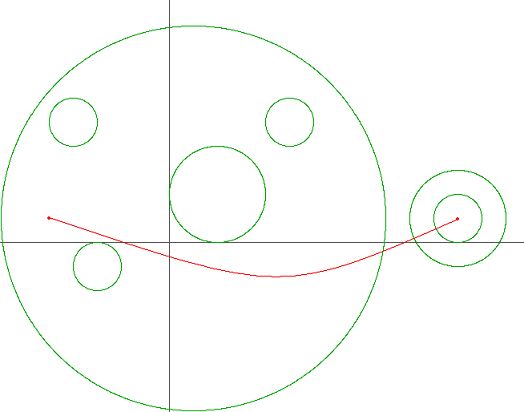
위 이미지는 백준 문제에서 제공한 예시 이미지다. 빨간 선이 어린 왕자가 출발점에서 도착지점까지 행성을 이탈하고 진입하는 횟수를 최소화하는 경로이다. 경로는 무수히 많으며 최단경로를 구 할 필요는 없다.
주어지는 값은 출발점 (x1, y1)과 도착점 (x2, y2)이 주어지며 행성들의 x,y좌표와 반지름이 주어진다. 각각의 행성들은 붙거나 겹치지 않는 값이 주어진다. 출발점과 도착점이 행성의 경계에 닿아 있을 경우 이는 진입이나 이탈로 판정하지 않는다. 진입 이탈이라는 말때문에 헷갈릴 수 있는데 그냥 도착지점까지 최소한 몇 개의 경개선을 지나는가를 구해야 하는 것이다.
이 문제는 1002번의 터렛 문제를 본인의 힘으로 풀었다면 얼마든지 풀 수 있는 문제인 것 같다. 위 예시 이미지를 보면 알겠지만.. 대충 봐도 출발점과 도착점을 감싸고 있는 원이 몇 개인가를 구하면 경계선을 몇 번 뚫고 가는지 나올 것 같다. 예외 상황이 있을 수 있으니 그래프로 점검해보자.

예제 입력값을 기준으로 시작점과 도착점 원을 생성하면 아래와 같이 나온다.

예제 이미지랑 똑같은 그래프가 나왔다. 이경우는
시작점을 포함하고 있는 원 + 도착점을 포함하고 있는 원
1 + 2 = 3 이된다.

이 예제의 좌표는 행성이 8개이지만 나는 그래프에 동그라미를 7개밖에 안 그려 놨기 때문에 7개만 사용해서 출력해본다.

이 그래프가 예외가 있는지 체크해보자.
시작점을 감싸고 있는 원 + 도착점을 감싸고 있는 원
3+1 = 4
위 공식이 맞는지 선을 그어서 확인해보자.

선이 행성 경계를 4번 지난다. 이쯤 되면 우리가 사용하는 공식이 맞는 것 같다.
다른 경우를 체크해보자.

행성이 12개 있다.... 귀찮지만 12개를 만들어줬다. 아래와 같이 나온다.

이 또한 선을 그어보면 알겠지만 우리가 작성한 공식에서 벗어나지 않는다.
예제를 그래프화 하면 다른 조건도 나오리라 생각했지만.. 그림판으로 예외조건을 그려보겠다..

파란 점이 출발점이고 빨간 점이 도착점이라 하자. 파란 점을 감싸는 원은 4개가 있고 빨간 점을 감싸는 원은 5개가 있다.
4 + 5 = 9
가 나온다. 선을 그어보면 알겠지만.. 경계선은 5번만 지나면 끝이다.
출발점을 감싸는 원의 수를 A로 칭하고 도착점을 감싸는 원의 수를 B로 칭하고 결괏값을 C로 칭하면
A + B = C
여기서 간과한 점은 출발점과 도착점을 동시에 감싸는 원이 있다. 이 원은 지날 필요가 없으므로 빼줘야 한다.
동시에 감싸는 원을 D라고 한다면
( A - D ) + ( B - D) = C
가 된다.
둘 다 동시에 감싸는 원의 수는 제외시켜야 한다.
출발점을 감싸는 원을 구하는 방법은 원의 중심점과 출발점의 거리를 구하고 그 값을 반지름의 길이와 비교해보면 된다.

행성 A와 B가 있고 출발점은 빨간 점이다. 초록 색선이 A와 출발점의 거리며 보라 색선은 A행성의 반지름이다.
출발점과 거리가 반지름보다 짧으면 행성에 포함된다.
B행성을 보면 반지름보다 출발점과의 거리가 더 크다. 이 경우에는 행성에 포함되지 않는다.
A행성에 출발점이 포함되어있는지 확인하는 조건은 아래와 같다.
출발점과의 거리 < 행성 반지름 (반지름과 같을 경우는 경계선이므로 판정에서 제외된다.)
설명을 두서없이 해서 이해하기 어려울 거 같다... 일단 정리하면
출발점 x1, y1, 도착점 x2, y2
행성 좌표 cx, cy, 행성 반지름 r
행성과 출발점의 거리 d1
행성과 도착점의 거리 d2
출발점이나 도착점 둘 중 하나만을 감싸고 있는 원의 수 합 count
행성과 출발점의 거리 => (x1 - cx)^2 + (y1 - cy)^2 = d1^2
행성과 도착점의 거리 => (x2 - cx)^2 + (y2 - cy)^2 = d2^2
행성이 출발점을 감싸는 조건 => d1 < r
행성이 도착점을 감싸는 조건 => d2 < r
두 지점을 동시에 감쌀 때 => 이경우는 제외하여야 하기 때문에 count에 아무런 변화를 주지 않는다.
두 지점을 동시에 감싸지 않을 때 => 이경우도 제외하여야 하기 때문에 count에 아무런 변화를 주지 않는다.
출발점 혹은 도착점을 감싸는 조건을 충족할 때 => count++
ㄴ 즉 (d1 < r) 과 (d2 < r) 이 서로 다를때 카운트를 올려주면된다.
(d1 < r) xor (d2 < r) => count++

코드를 짜보자.
행성이 몇 개가 나올지 모르므로 루프를 돌려 변수 cx, cy, r를 돌려쓸 예정이다. 해당 세 변수는 행성 값을 입력받을 때마다 이전 입력값을 기억하지 못하기 때문에 입력을 받았을 때 계산을 끝내고 카운트를 바로바로 올려준다.
행성 좌표 입력이 종료되면 루프도 종료할 것이고 이때 카운트한 수를 출력해주면 코딩 끝!
#include <iostream>
#include <cmath>
int main() {
int t, n, x1, y1, x2, y2, cx, cy,r, count;
double d1, d2;
std::cin >> t;
while (t--) {
count = 0;
std::cin >> x1 >> y1 >> x2 >> y2;
std::cin >> n;
while (n--) {
std::cin >> cx >> cy >> r;
d1 = sqrt(pow(x1 - cx, 2) + pow(y1 - cy, 2));
d2 = sqrt(pow(x2 - cx, 2) + pow(y2 - cy, 2));
if ((d1 < r) xor (d2 < r)) {
count++;
}
}
std::cout << count << "\n";
}
return 0;
}콘솔 창에 입력하여 테스트하였다. 예제대로 입력해보니 출력이 정상적으로 된다. 스샷은 못 찍었다... 너무 길고 복잡해 스샷을 봐도 도움이 되진 않을 것이다.. 해당 코드를 등록해보자.

...오오오오..... 처음으로 한 번만에 성공했다.... 16ms가 상당히 거슬린다...
다른 사람들 결과를 보니 0ms가 가능하다.
0ms 코드를 보니 역시나.. scanf와 printf를 사용한다.
iostream의 설정을 바꿔 iostream도 0ms로 실행한 사람도 있다.
그냥 익숙한 방법인 scanf와 printf를 사용하여 0ms가 되는지 체크해보자.
#include <stdio.h>
#include <cmath>
int main() {
int t, n, x1, y1, x2, y2, cx, cy,r, count;
double d1, d2;
scanf("%d", &t);
while (t--) {
count = 0;
scanf("%d%d%d%d%d", &x1,&y1,&x2,&y2,&n);
while (n--) {
scanf("%d%d%d", &cx, &cy, &r);
d1 = sqrt(pow(x1 - cx, 2) + pow(y1 - cy, 2));
d2 = sqrt(pow(x2 - cx, 2) + pow(y2 - cy, 2));
if ((d1 < r) xor (d2 < r)) {
count++;
}
}
printf("%d\n", count);
}
return 0;
}
0ms 성공이다. 입출력 횟수가 많아질수록 iostream의 성능이 떨어지는 것 같다.
iostream의 설정을 변경하여 빠르게 만드는 방법이 있다. 이 부분은 나중에 따로 글로 작성하겠다. 검색해도 많은 글이 나오니 급하시면 검색하시라~!